Aplicações de diagonalização¶
Aula síncrona 26/out/2020
Referências¶
Boldrini 7.1.5
Callioli Parte 2 – 5.6
Osciladores acoplados¶
Resumo¶
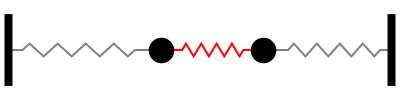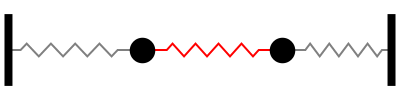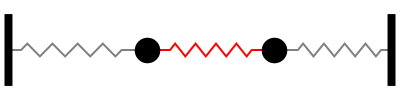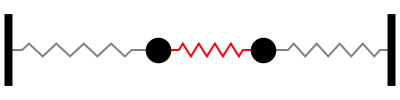
Considere um sistema de dois blocos de massa \(m_1\) e \(m_2\) ligados por molas de constante elástica \(k_1\), \(k_2\) e \(k_3\) conforme a imagem abaixo, extraída de [Boldrini]
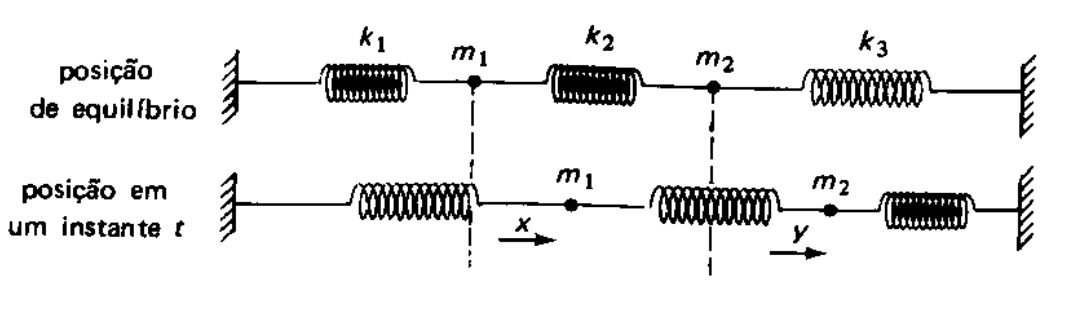
Os deslocamentos dos blocos em relação à posição de equilíbrio são \(x\) para o bloco 1 e \(y\) para o bloco 2.
A segunda lei de Newton para cada um dos blocos será:
\[\begin{split}\begin{cases} m_1 \ddot{x} &= -k_1 x + k_2 (y-x) \\ m_2 \ddot{x} &= -k_2 (y-x) + k_3 y \end{cases}\end{split}\]Nota
Utilizamos a notação de Newton para derivadas, onde cada ponto sobre a variável indica uma derivação em relação ao tempo, então:
\[\begin{split}\begin{aligned} \dot{x} &= \frac{\operatorname{d} x}{\operatorname{d} t}\\ \ddot{x} &= \frac{\operatorname{d}^2 x}{\operatorname{d} t^2}\\ \end{aligned}\end{split}\]Esse sistema pode ser escrito de forma matricial:
\[\begin{split}\begin{bmatrix} \ddot{x} \\ \ddot{y} \end{bmatrix} = \begin{bmatrix} - \frac{k_1 + k_2}{m_1} & \frac{k_2}{m_1} \\ \frac{k_2}{m_2} & - \frac{k_2 + k_3}{m_2} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\end{split}\]Supondo massas e molas idênticas: \(m_1 = m_2 = m\) e \(k_1 = k_2 = k_3 = k\), temos
\[\begin{split}\begin{bmatrix} \ddot{x} \\ \ddot{y} \end{bmatrix} = \begin{bmatrix} - \frac{2 k}{m} & \frac{k}{m} \\ \frac{k}{m} & - \frac{2k}{m} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\end{split}\]Podemos diagonalizar a matriz desse sistema e reescrever as equações na base de autovetores \(B = \left\{\vec{n}_1, \vec{n}_2\right\}\) e coordenadas \(\begin{bmatrix}p\\q\end{bmatrix}_B\). Assim, o sistema fica
\[\begin{split}\begin{bmatrix} \ddot{p} \\ \ddot{q} \end{bmatrix}_B = \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}_B \begin{bmatrix} p \\ q \end{bmatrix}_B\end{split}\]Os autovalores são: \(\lambda_1 = \frac{-k}{m}\) e \(\lambda_2 = \frac{-3k}{m}\) e os respectivos autovetores são \(\vec{n}_1 = (1,1)\) e \(\vec{n}_2 = (1,-1)\).
O sistema de equações diferenciais, desacoplado, fica
\[\begin{split}\begin{cases} \ddot{p} &= -\dfrac{k}{m} q \\ \ddot{q} &= -\dfrac{3k}{m} q \end{cases}\end{split}\]Cada equação é um oscilador harmônico simples independente e pode ser resolvida separadamente, com soluções (verifique!)
\[\begin{split}p(t) & = A \sin \left(\sqrt{\frac{k}{m}} t\right) + B \cos \left(\sqrt{\frac{k}{m}} t\right) \\ q(t) & = C \sin \left(\sqrt{\frac{3k}{m}} t\right) + D \cos \left(\sqrt{\frac{3k}{m}} t\right)\end{split}\]A variável \(p\) representa a posição do centro de massa dos blocos, de forma que o sistema se comporta como se fosse um único bloco em uma oscilação harmônica simples. Chamamos este comportamento de primeiro modo normal. Ilustramos esse sistema com as animações produzidas pelo Prof. Daniel [Russell] da Penn State University
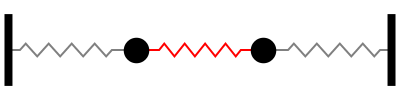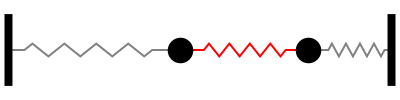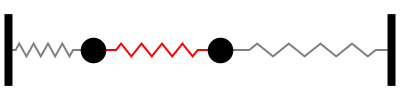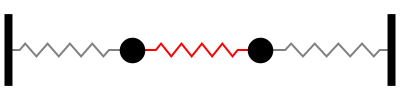
A variável \(q\) representa a distância entre dos blocos, de forma que os blocos oscilam simetricamente em torno do centro de massa, em direções opostas. Chamamos este comportamento de segundo modo normal. A frequência de oscilação desse modo é três vezes maior que a frequência do primeiro modo normal.
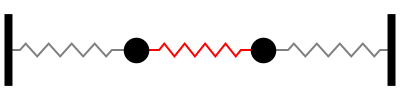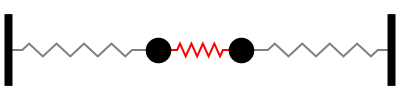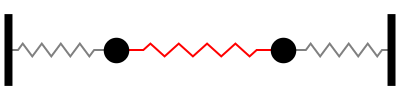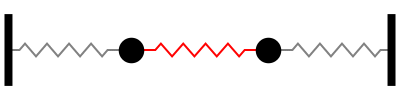
No segundo modo normal de vibração, o ponto central da mola que liga os blocos não se move. Chamamos esse ponto de nó.
A solução geral vai envolver uma combinação linear desses dois modos normais, resultando em movimentos mais complexos, mas que ainda podem ser entendidos como a associação de um movimento do centro de massa mais um movimento de afastamento/aproximação dos blocos:
Sistemas mais complexos podem ser entendidos dessa forma. Uma placa de metal, por exemplo, pode ser entendida como infinitos blocos ligados com molas e as oscilações naturais (ressonâncias) serão esses modos normais. Quanto maior a frequência, mais nós:
Videoaula¶
Video complementar¶
- Prof. Dan Russell – Mode Shapes for Multiple Degree-of-Freedom Oscillators
- Prof. Dan Russell — Coupled pendulum
- Figuras de Chladni - Lindos padrões aleatórios desenhados com Cuscuz!
- Pêndulos Duplos São Malucos
Lista de exercícios¶
Referências¶
- Boldrini
Boldrini; Costa; Figueiredo; Wetzler Álgebra Linear, 3a edição, Editora Habra
- Russell
Acoustics and Vibration Animations - Dan Russell, Grad. Prog. Acoustics, Penn State