17. Transformações lineares e a geometria do \(\mathbb{R}^2\)¶
Questionário: terça, 10 de agosto de 2021
Aula síncrona: quinta, 12 de agosto de 2021
17.1. Bibliografia¶
Boldrini 5.2
Strang 8.7
17.2. Transformações lineares na geometria¶
Escala (expansão/contração) no \(\mathbb{R}^2\) e no \(\mathbb{R}^3\)
Reflexão em torno de um eixo/plano
Rotação de um ângulo \(\theta\) em torno da origem
Cisalhamento horizontal/vertical no \(\mathbb{R}^2\)
Cisalhamento entre planos no \(\mathbb{R}^3\)
17.2.1. Resumo¶
Nota
Representaremos os vetores do \(\mathbb{R}^2\) como pontos no plano e os de \(\mathbb{R}^3\) como pontos no espaço. (A convenção de extremidade de um vetor que aprte da origem, como em VGA). As transformações a seguir são utilizadas em computação gráfica, por exemplo, para modificar imagens, determinadas por conjuntos de pontos/vetores. Entenda as modificações nas figuras como o efeito da transformação em cada um dos pontos (pixels) da imagem.
As representações matriciais serão escritas inicialmente considerando a base canônica.
- Escala
Transformação que modifica (escala/escalona) os vetores, multiplicando sua norma por um fator positivo \(\lambda\) constante. Resulta em uma expansão se \(\lambda > 1\) e em uma contração se \(\lambda < 1\)
\[\begin{split}\begin{aligned} S &: \mathbb{R}^2 \to \mathbb{R}^2 & S(x,y) &= \lambda(x,y)\\ \end{aligned}\end{split}\]A matriz de uma transformação de escala fica
\[\begin{split}\begin{bmatrix}S\end{bmatrix} = \begin{bmatrix}\lambda & 0 \\ 0 & \lambda \end{bmatrix}\end{split}\]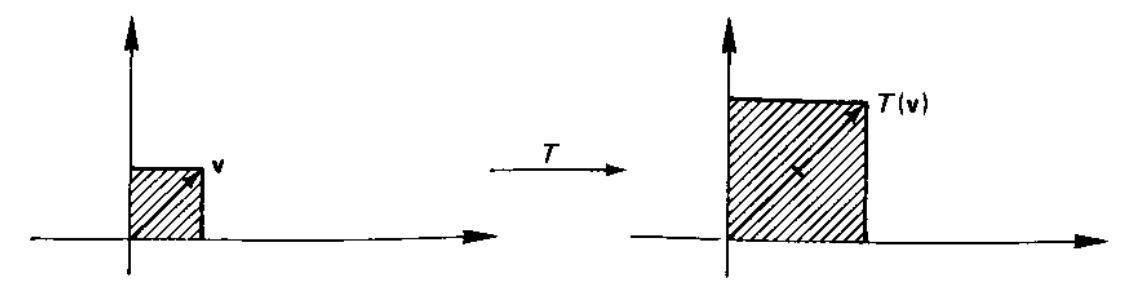
Transformação de expansão. [Boldrini]¶
- Escala assimétrica ao longo de um eixo
Neste caso, apenas uma das componentes é expandida/contraída. É a transformação que leva, por exemplo, um quadrado a um retângulo, ou um cubo a um paralelepípedo com faces retangulares.
- Em \(\mathbb{R}^2\), expandido ao longo do eixo \(x\):
- \[\begin{split}\begin{aligned} S_x(x, y) &= (2x, y) & \begin{bmatrix}S_x\end{bmatrix} &= \begin{bmatrix}2 & 0 \\ 0 & 1 \end{bmatrix} \end{aligned}\end{split}\]
- Em \(\mathbb{R}^3\), contraindo ao longo do eixo \(z\):
- \[\begin{split}\begin{aligned} S_z(x, y, z) &= \left(x, y, \frac{1}{3}z\right) & \begin{bmatrix}S_z\end{bmatrix} &= \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \frac{1}{3} \end{bmatrix} \end{aligned}\end{split}\]
- Reflexão em torno de um eixo/plano
Esta transformação leva os pontos de um lado do eixo/plano aos pontos simétricos no lado oposto. Algebricamente é uma troca de sinal da componente ortogonal ao eixo/plano.
- Em \(\mathbb{R}^2\), uma reflexão em relação ao eixo \(x\):
- \[\begin{split}\begin{aligned} R_x(x, y) &= (x, -y) & \begin{bmatrix}S_x\end{bmatrix} &= \begin{bmatrix}1 & 0 \\ 0 & -1 \end{bmatrix} \end{aligned}\end{split}\]
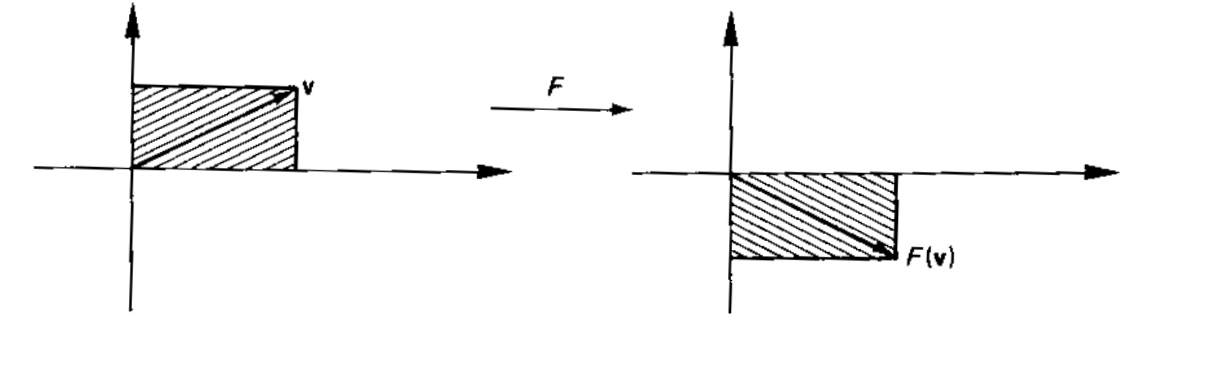
Reflexão em relação ao eixo \(x\). [Boldrini]¶
- Em \(\mathbb{R}^3\), uma reflexão em relação ao plano \(yz\):
- \[\begin{split}\begin{aligned} R_{yz}(x, y, z) &= (-x, y, z) & \begin{bmatrix}R_{yz}\end{bmatrix} &= \begin{bmatrix}-1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned}\end{split}\]
Nota
A reflexão não muda a norma dos vetores. O efeito é como se houvesse um espelho no plano de reflexão.
Nota
No \(\mathbb{R}^2\), a reflexão se dá em relação a um eixo e no \(\mathbb{R}^3\) a reflexão se dá em relação a um plano. Em ambos os casos, apenas o sinal de uma componente muda.
No \(\mathbb{R}^3\) é possível realizar a reflexão em relação a um eixo, mas essa transformação é o resultado de reflexões em cada um dos planos gerados por esse eixo, portanto cnsideramos a reflexão em um plano como primitiva.
- Reflexão (inversão) na origem
Leva cada vetor a seu oposto:
\[\begin{split}\begin{aligned} T(x, y, z) &= (-x, -y, -z) & \begin{bmatrix}T\end{bmatrix} &= \begin{bmatrix}-1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{bmatrix} \end{aligned}\end{split}\]
Inversão pela origem. [Boldrini]¶
- Rotação de um ângulo \(\theta\):
Os vetores são girados por uo ângulo :math: theta em torno da origem, no caso do \(\mathbb{R}^2\), ou em torno de um eixo (que passa pela origem) no caso do \(\mathbb{R}^3\). Os vetores do eixo não mudam.
- No plano:
- \[\begin{split}\begin{aligned} R_\theta(x, y) &= (x \cos(\theta) - y \sin(\theta), y \cos(\theta) + x \sin(\theta)) & \begin{bmatrix}R_\theta\end{bmatrix} &= \begin{bmatrix}\cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \end{aligned}\end{split}\]
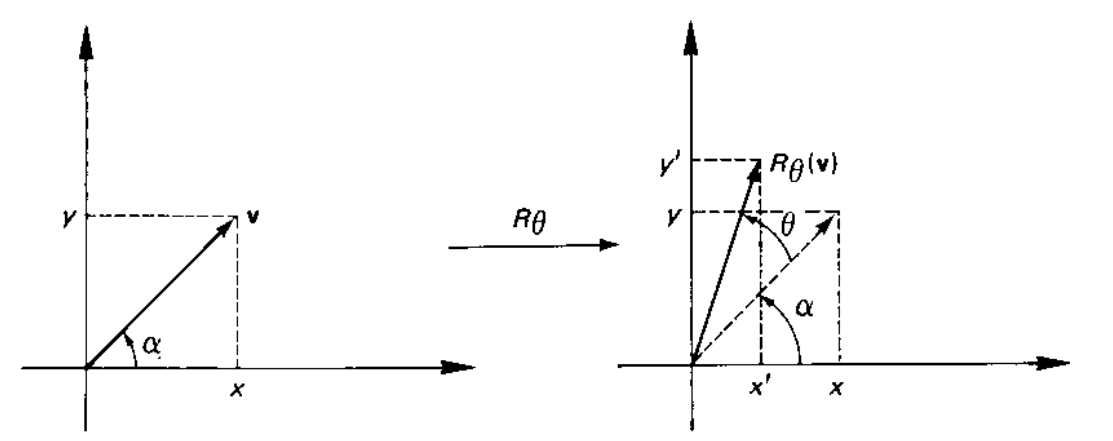
Rotação de um ângulo \(\theta\) em relação à origem. [Boldrini]¶
- No espaço, em torno do eixo \(z\):
No plano \(xy\), a rotação ocorre como no caso do \(\mathbb{R}^2\), enquanto a componente \(z\) não muda:
\[\begin{split}\begin{aligned} R_{\theta, z}(x, y, z) &= (x \cos(\theta) - y \sin(\theta), y \cos(\theta) + x \sin(\theta), z) & \begin{bmatrix}R_{\theta, z}\end{bmatrix} &= \begin{bmatrix}\cos(\theta) & -\sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned}\end{split}\]- No espaço, em torno do eixo \(x\):
No plano \(yz\), a rotação ocorre como no caso do \(\mathbb{R}^2\), enquanto a componente \(x\) não muda, então a matriz de rotação aparece “deslocada”:
\[\begin{split}\begin{bmatrix}R_{\theta, x}\end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) \\ 0 & \sin(\theta) & \cos(\theta) \end{bmatrix}\end{split}\]
- Cisalhamento no \(\mathbb{R}^2\)
Transformação que leva retângulos a paralelogramos. Linhas/planos paralelos à direção de cisalhamento não mudam, mas a direção ortogonal passa a ter uma inclinação determinada pelo fator de cisalhamento \(m\):
- Cisalhamento horizontal
Ao longo do eixo \(x\):
\[\begin{split}\begin{aligned} C_x (x,y) &= (x + my, y) & \begin{bmatrix}C_x\end{bmatrix} &= \begin{bmatrix} 1 & m \\ 0 & 1 \end{bmatrix} \end{aligned}\end{split}\]
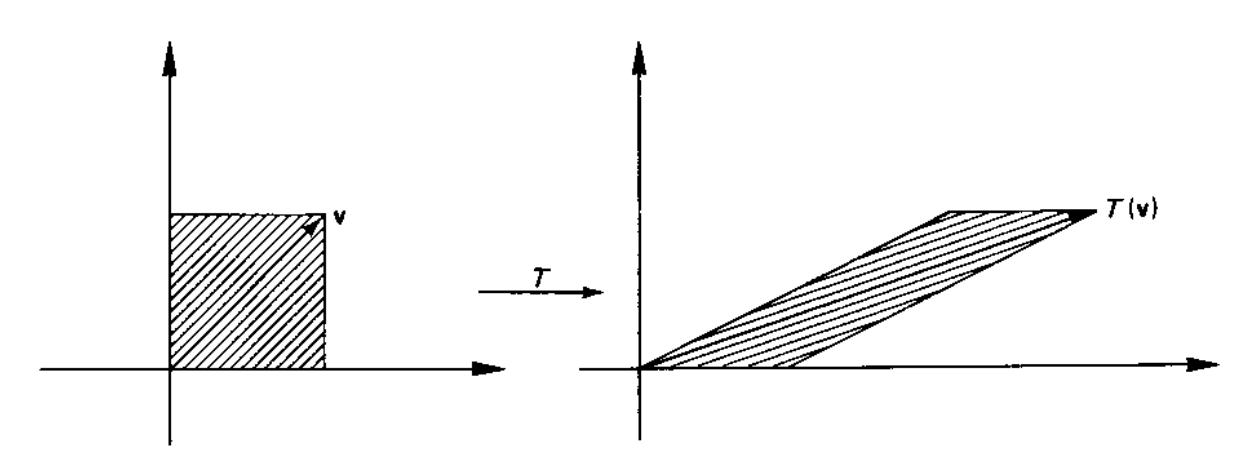
Cisalhamento horizontal. [Boldrini]¶
- Cisalhamento vertical
Ao longo do eixo \(y\):
\[\begin{split}\begin{aligned} C_y (x,y) &= (x, y + mx) & \begin{bmatrix}C_y\end{bmatrix} &= \begin{bmatrix} 1 & 0 \\ m & 1 \end{bmatrix} \end{aligned}\end{split}\]
Nota
No cisalhamento horizontal/vertical puro, a altura/largura da figura não se altera.
- Cisalhamento no \(\mathbb{R}^3\)
No espaço, o cisalhamento se dá pelo deslocamento de planos paralelos em uma direção dada, conforme o exemplo:
- Cisalhamento no plano \(xy\) ao longo da direção \(x\):
- \[\begin{split}\begin{aligned} C_{xy,x} (x,y, z) &= (x + mz, y, z) & \begin{bmatrix}C_y\end{bmatrix} &= \begin{bmatrix} 1 & 0 & m \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned}\end{split}\]
17.2.2. Videoaula¶
17.3. Transformações afins e coordenadas homogêneas¶
Translação como transformação não-linear
Coordenadas homogêneas como projeção
Translação em coordenadas homogêneas: operador linear
Demais transformações em coordenadas homogêneas
Composição de transformações
17.3.1. Resumo¶
Em breve…