5. Período de do pêndulo e aceleração da gravidade¶

18 de setembro de 2025

5.1. Objetivos¶

Medir período (T) de oscilação do pêndulo simples;
Inferir a função T(L), onde L é o comprimento do pêndulo simples;
Determinar a aceleração da gravidade;
Compreender o conceito de ajuste de curva/linha de tendência.

5.2. Roteiro¶

Acesse aqui o roteiro da atividade. Lembre-se de ler o roteiro com antecedência e levar uma cópia impressa para a aula.

Nesta atividade utilizaremos planilhas eletrônicas para armazenar e processar as medidas. Utilize as planilhas do Google e compartilhe com os colegas e o com o professor.

Nota

Recomendo que você utilize sua conta institucional @ufrn.br para facilitar o compartilhamento das planilhas com os colegas e com o professor.

5.3. Conteúdo¶

5.3.1. Ajuste de retas¶

Como vimos na atividade anterior, toda medida está associada a um erro e quando realizamos medidas repetidas da mesma grandeza existe uma variação natural no valor medido, uma dispersão das medidas. Isso significa que nunca medimos o valor verdadeiro de uma grandeza.

Suponha agora que desejamos caracterizar uma grandeza em função de outra, por exemplo, determinar o efeito que a variável independente \(x\) tem sobre o valor da variável dependente \(y\). Para isto, montamos um aparato experimental em que conseguimos fixar valores de \(x\) e realizamos medidas de \(y\) associadas a diferentes valores de \(x\). No caso do experimento do pêndulo, o comprimento do pêndulo é a variável independente \(x\) e o período, a variável dependente \(y\).

Veja abaixo o gráfico dos dados de um experimento como o da aula de hoje e da função \(T(L) = 2\pi \sqrt{\frac{L}{g}}\), com valor de \(g\) ajustado aos dados. Note que os dados não se encontram exatamente sobre a curva, mas distribuídos em torno dela.

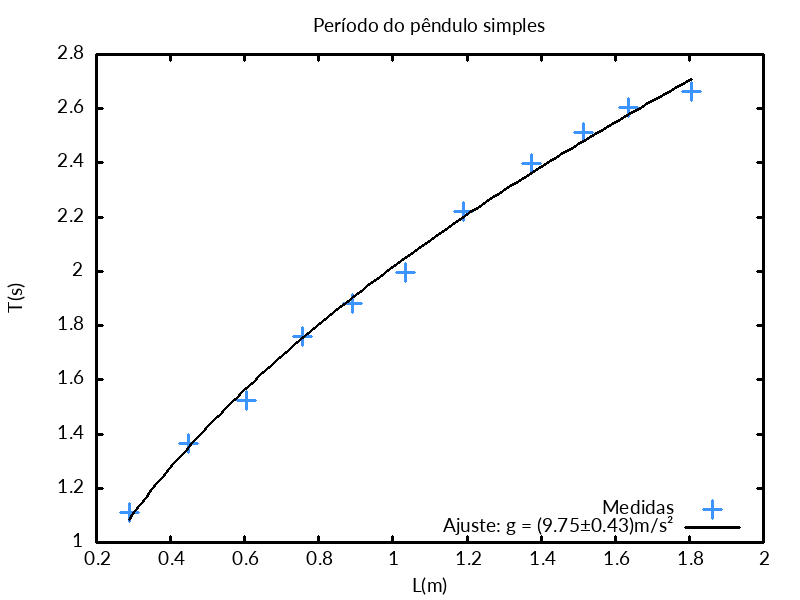
Construímos, então, a partir da teoria, ou da análise da aparência do gráfico \(y \times x\), um modelo para a relação:

\[y = f(x)\]

A função \(f(x)\) pode tomar diversas formas, a depender da relação entre as grandezas envolvidas. As mais comuns tipicamente são:

\[\begin{split}\text{Linear: } f(x) &= ax + b \\ \text{Quadrática: } f(x) &= ax^2 + bx + c \\ \text{Lei de potência: } f(x) &= ax^b \\ \text{Polinomial: } f(x) &= \sum_{i=0}^{n} a_i x^i \\ \text{Exponencial: } f(x) &= a e^{bx} \\ \text{Logarítmica: } f(x) &= a \log{(bx)},\end{split}\]

Onde \(a\), \(b\), \(c\), \(a_i\) etc. são os parâmetros da função. Caracterizar a variável consiste em determinar esses parâmetros para que a função \(y=f(x)\) melhor se ajuste aos dados. A esse procedimento damos o nome de ajuste de curva, ajuste de função ou curve fitting em inglês.

Tipicamente, o algoritmo utilizado para isso é o Método dos Mínimos Quadrados, em que se busca parâmetros que minimizem a soma dos quadrados da diferença entre os valores previstos pela função \(y=f(x)\) e o valor medido experimentalmente \(y_i\):

\[\chi^2 = \sum_i (y - y_i)^2\]

O Método dos Mínimos Quadrados em si é assunto dos cursos Álgebra Linear e Computação Numérica e não vamos abordá-lo aqui. Caso tenha interesse em seu funcionamento, você pode acompanhar a aula no curso de Álgebra Linear.

5.3.2. Ajuste de reta nas Planilhas Eletrônicas¶

Neste curso, vamos efetuar ajuste de funções lineares, ou ajustes de retas, nas Planilhas do Google. Estas instruções também são válidas para o LibreOffice Calc e, provavelmente, para o Microsoft Excel.

Nas Planilhas do Google e no LibreOffice, o ajuste de retas do tipo \(y = ax + b\) a dados é feita com a função PROJ.LIN (se você configurou seu aplicativo para nomes de fórmula em inglês, o nome é LINEST). Essa função recebe até quatro argumentos:

Função PROJ.LIN(dados_y; [dados_y]; [calcula_b]; [detalhado]):

Ajusta uma reta aos dados utilizando o método de mínimos quadrados. Os parâmetros entre colchetes são opcionais.

dados_y

Os valores da variável \(y\), do eixo vertical do gráfico (na figura abaixo, a região B3:B7)

dados_x

Os valores da variável \(x\), do eixo horizontal do gráfico (na figura abaixo, a região :A3:A7)

calcula_b

Se esse valor for 1, o valor do coeficiente linear \(b\) da reta também será ajustado. Se for 0, a função ajustada será \(f(x) = ax\) e a reta passará obrigatoriamente pela origem.

detalhado

Se este valor for 1, além dos valores ajustados de \(a\) e \(b\), a função devolverá as incertezas nos parâmetros ajustados e outras informações sobre o ajuste. Essas informações aparecem na imagem abaixo como exemplo. Em nossas atividades vamos apenas nos ocupar das 5 primeiras:

A: Coeficiente angular do ajuste
B: Coeficiente linear do ajuste (se calcula_b = 1)
σA: Incerteza do coeficiente angular
σB: Incerteza do coeficiente linear (se calcula_b = 1)
R²: Coeficiente de determinação do ajuste. É uma medida de qualidade: quanto mais próximo de 1, melhor o ajuste. É calculado como \(R² = 1 - \frac{RSS}{\chi^2}\).
σy: Incerteza no valor de \(y\) previsto pela função ajustada.
F: F-estatística, é outra medida da qualidade do ajuste.
DoF: Graus de liberdade: número de dados menos número de parâmetros ajustados
RSS: Soma dos quadrados da diferença entre os valores de \(y_i\) dos dados e a sua média: \(RSS=\sum_i \left(y_i - \bar{y}\right)^2\)
χ²: Soma dos quadrados da diferença entre os valores medidos \(y_i\) e o valor previsto pela função ajustada: \(\chi^2 = \sum_i (y_i - y(x_i))^2\). O método de mínimos quadrados busca minimizar este valor.

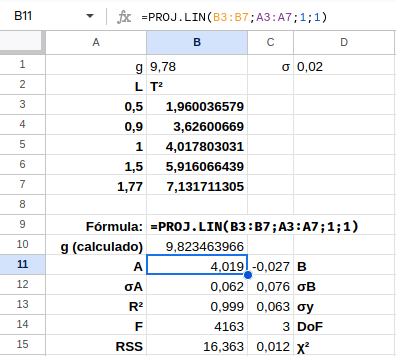
Note que a função PROJ.LIN preenche diversas células da planilha. No exemplo acima, a fórmula foi inserida na célula que está selecionada (B11) e preencheu 5 linhas e 2 colunas com valores (porque foi passado o valor 1 para o parâmetro detalhado), então inclua a função em um lugar que tenha espaço para esses valores. Com os valores nas células, você pode utilizá-los diretamente em outras fórmulas, como a célula B10 do exemplo, que calcula o valor de \(g = \frac{(2\pi)^2}{a}\) a partir do resultado do ajuste.

5.3.3. Tutoriais em vídeo¶

Tutorial básico de Planilhas do Google, pelo Prof. Pedro Ferreira

Gráficos e ajuste de retas
Ajuste de parábolas